Two new contributions: Deep learning and dynamics on networks
While still under lockdown due the COVID-19 pandemic, the Dynamica Lab remains as active as ever! Indeed, the group recently posted two new preprints discussing the use of Deep learning to access dynamical systems on networks and their applications:
- Detecting structural perturbations from time series with deep learning
- Deep learning of stochastic contagion dynamics on complex networks
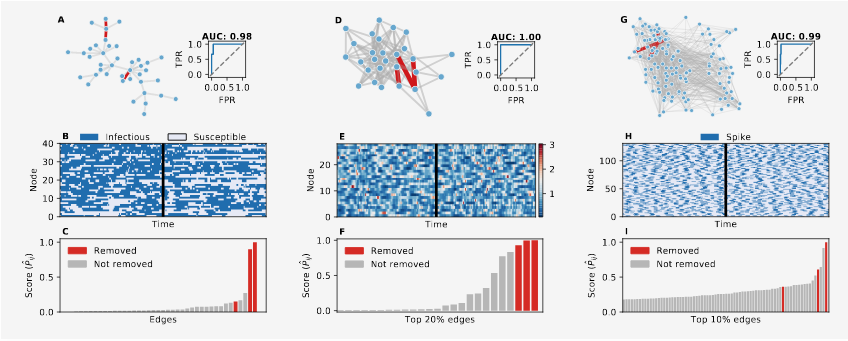
Detecting structural perturbations from time series with deep learning
Small perturbations in the structure of complex systems can lead to critical scenarios, from functional breakdowns in the brain to economic crises. Hence, our ability to prevent these situations is directly linked to our ability to detect these perturbations before the tipping point. To address this issue, this paper proposes a data-driven approach based deep learning to infer broken links directly from time series. As shown below, this extremely versatile tool is successfully applied to multiple cases, from epidemic spreading, to population and neural dynamics. The approach is proved highly effective in realistic settings involving noise in the time series and limited training data, while remaining computationally scalable to large systems.
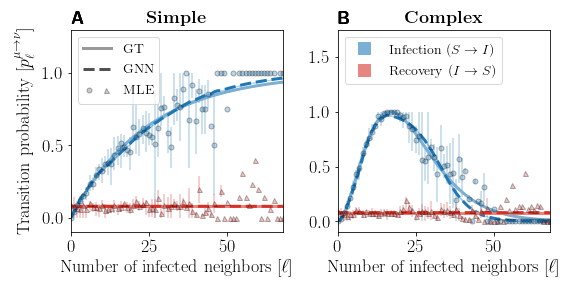
Deep learning of stochastic contagion dynamics on complex networks
Forecasting the propagation of infectious diseases is a complex problem, which is only partially addressed by simple mechanistic models. This paper presents a complementary and data-driven approach to modeling dynamics on networks using graph neural networks (GNN), ranging from simple contagion, to complex and interacting contagion. It is shown that GNNs can be trained to effectively reproduce the inner mechanisms of contagion dynamics—that is, their transition probabilities—with surprising accuracy (see below). The paper also addresses the possibility to use GNNs to gain insights about the critical behaviors of contagion dynamics from data—some kind of numerical Petri dish.