Paper published in Physical Review X

The latest contribution of the network section is available in the March issue of Physical Review X.

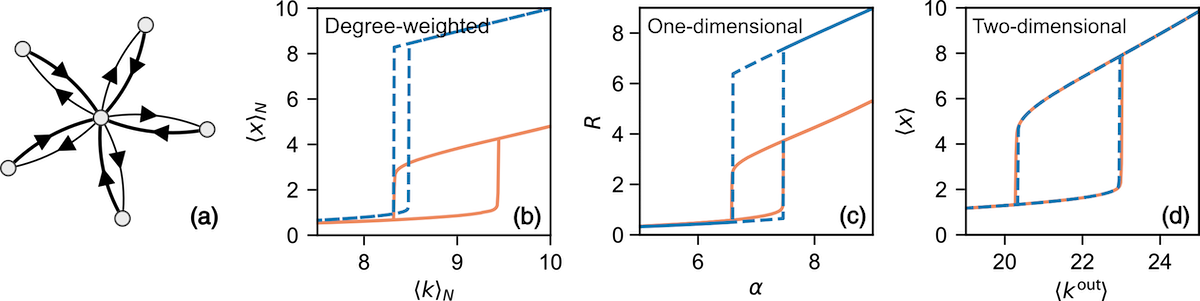
The paper entitled Spectral Dimension Reduction of Complex Dynamical Networks presents a mathematically sound formalism to coarse grain the high dimensional set of equations governing the evolution of a general deterministic dynamics on a network. The approach leverage the spectral properties of a network, more specifically the dominant eigenvalues and eigenvectors of the adjacency matrix, to perform the reduction. The lower dimensional system can be used to better understand the critical behavior of certain systems and lead the way towards a better comprehension of the robustness and the resilience of complex systems.

Links to the full text and preprints are available on the publication page.